Skip to content

Stochastic optimization.

Understanding the problem

theorical example 3dm

theorical example gh

HILL CLIMBING method

Undestending the method

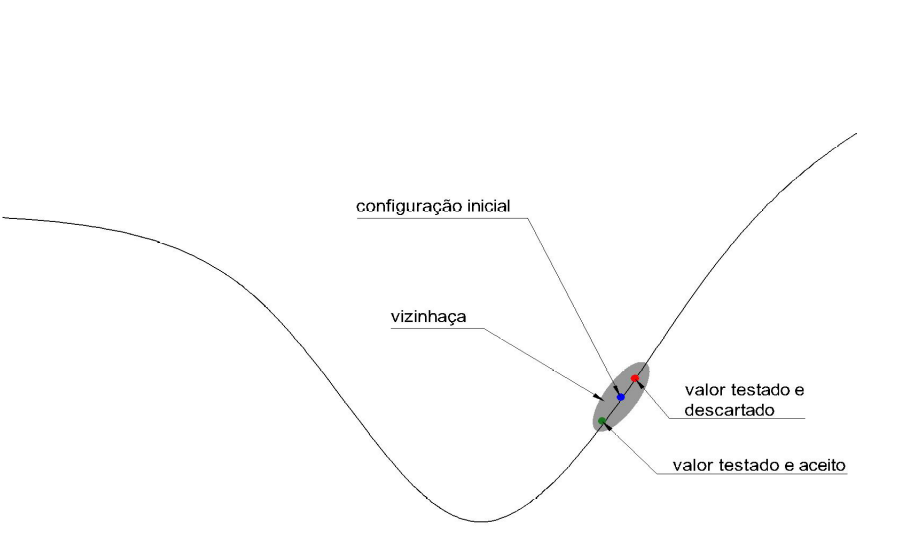
ilustra

Goal

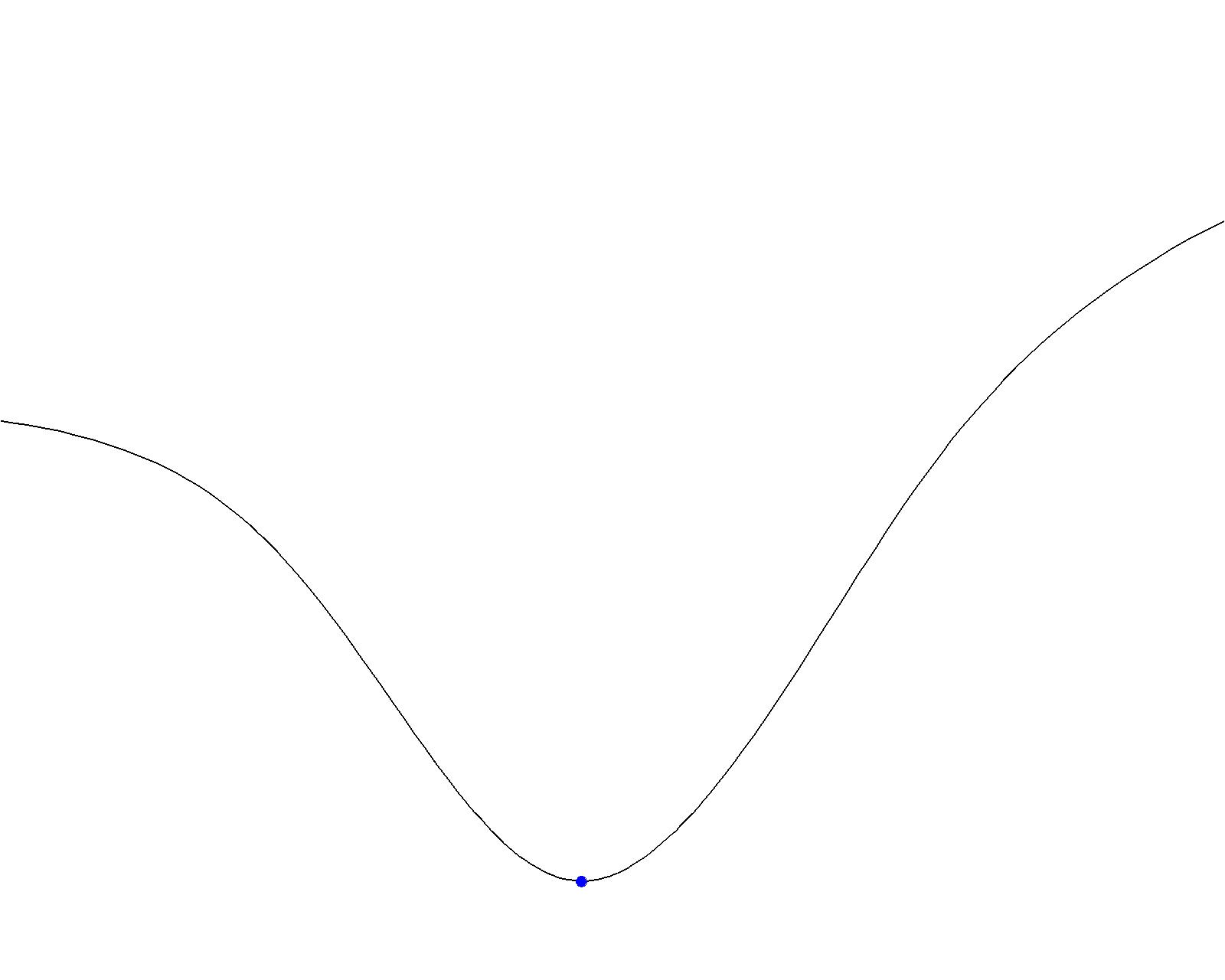
ilustra

Limitations

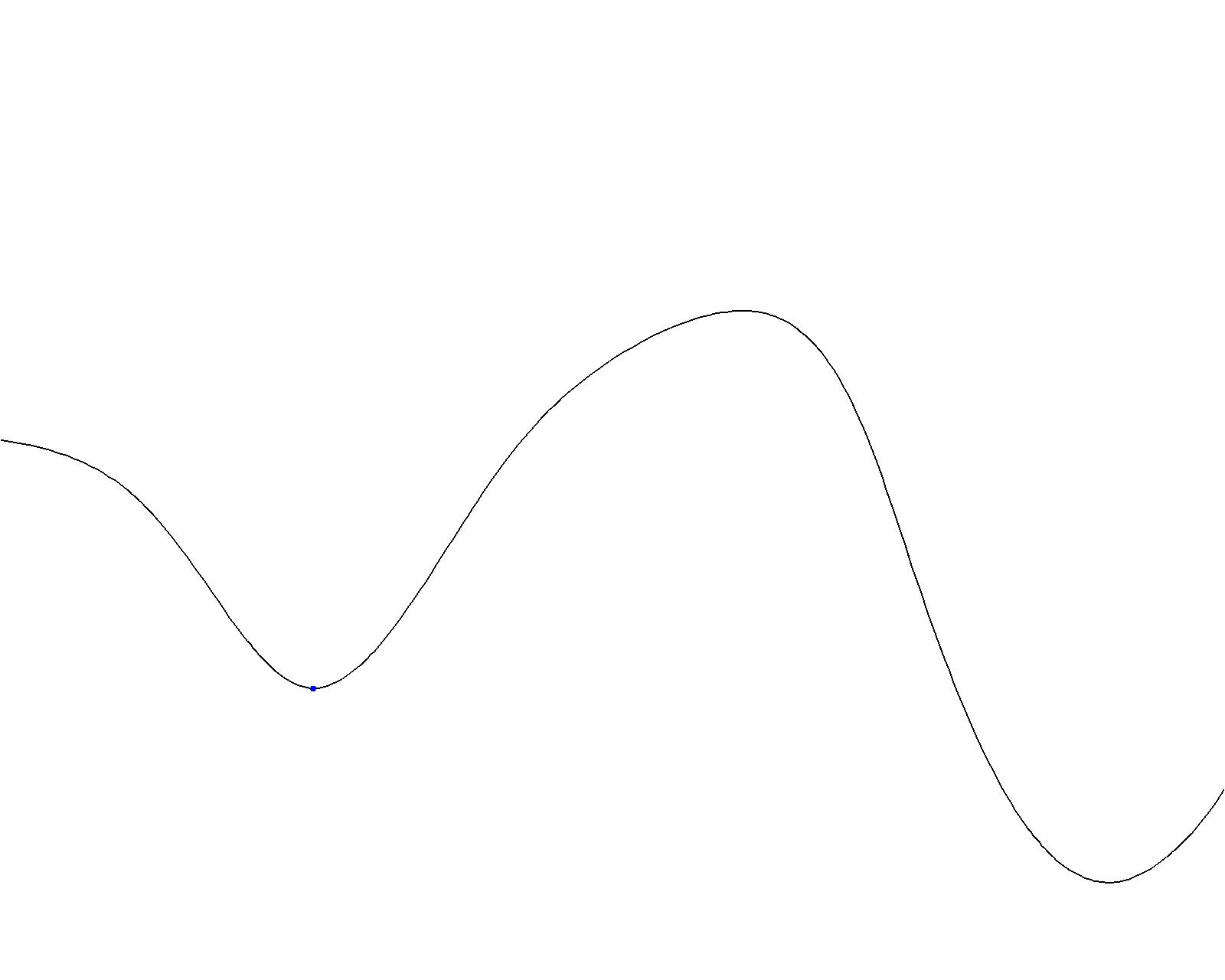
ilustra

Local and Global maximum and minimum

máximos e mínimus

source: https://upload.wikimedia.org/wikipedia/commons/6/68/Extrema_example_original.svg

Multivariate problems

multi var

source

Evolutionary Algorithms

Algoritmos Genéticos

  1. Fitness function

  2. Genes

  3. Population

  4. Generations

  5. Inbreeding

  6. Mutations

Galapagos Solver

arquivo 3dm

arquivo gh

The Galapagos component is in the tab Params, section uitl.

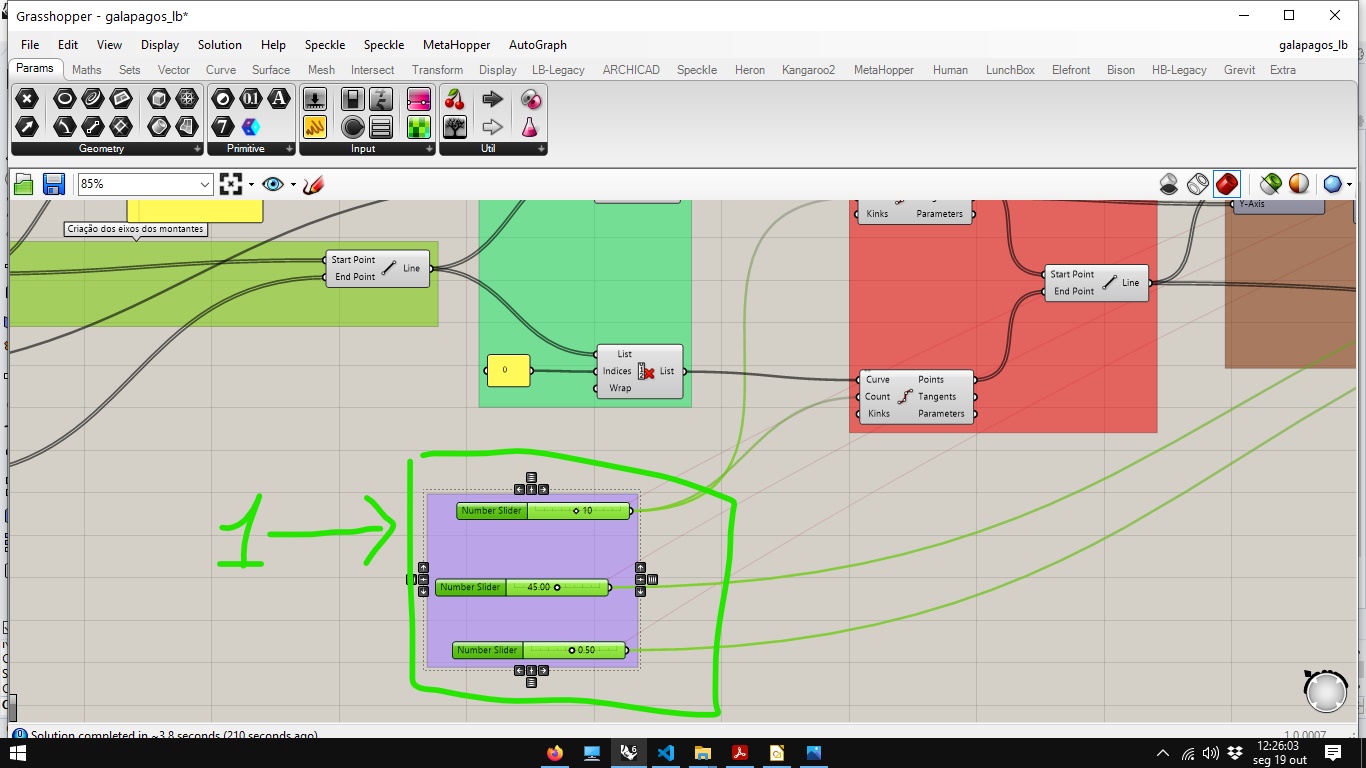
galapagos_01

The most practical way to indicate optimization parameters for the algorithm is: first select all the sliders you want to optimize.

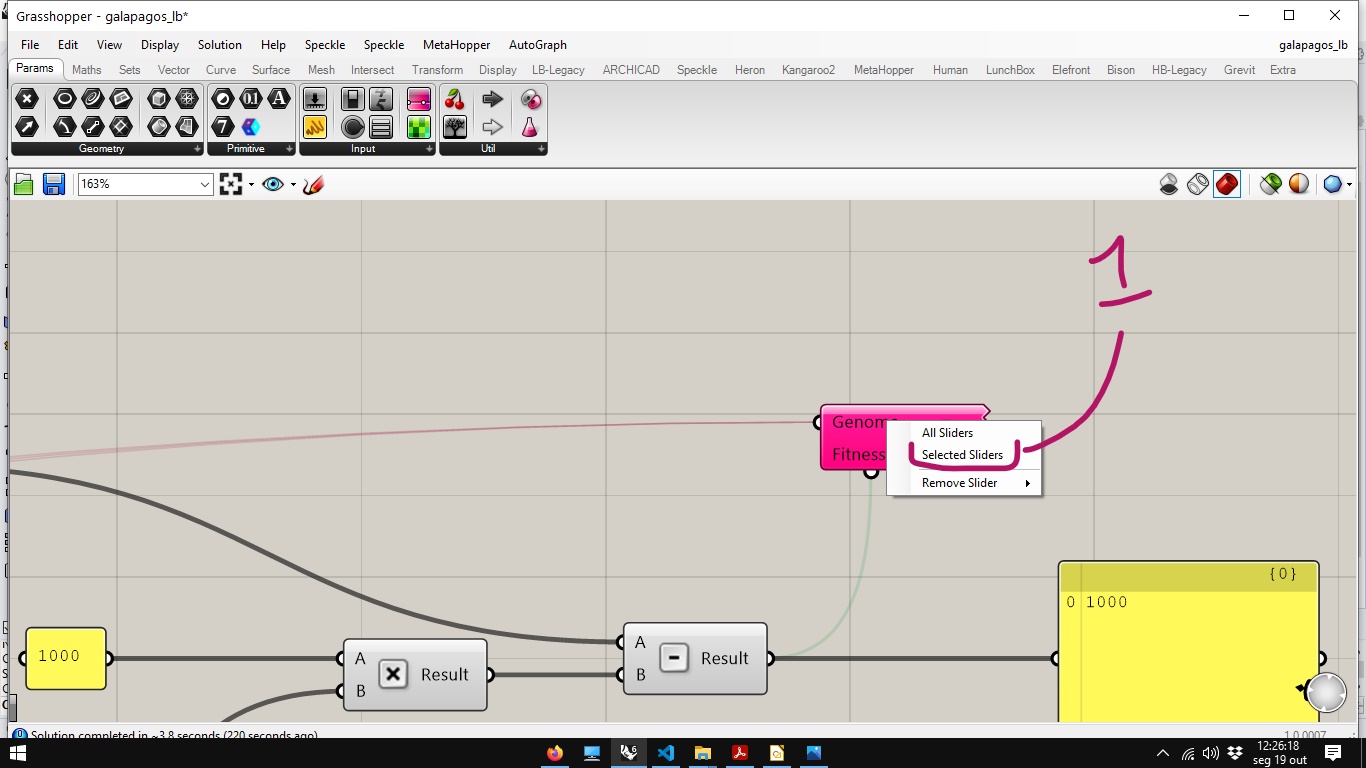
galapagos_01

Then right-click on the genome input of the Galapagos component and choose the *Selected Sliders option

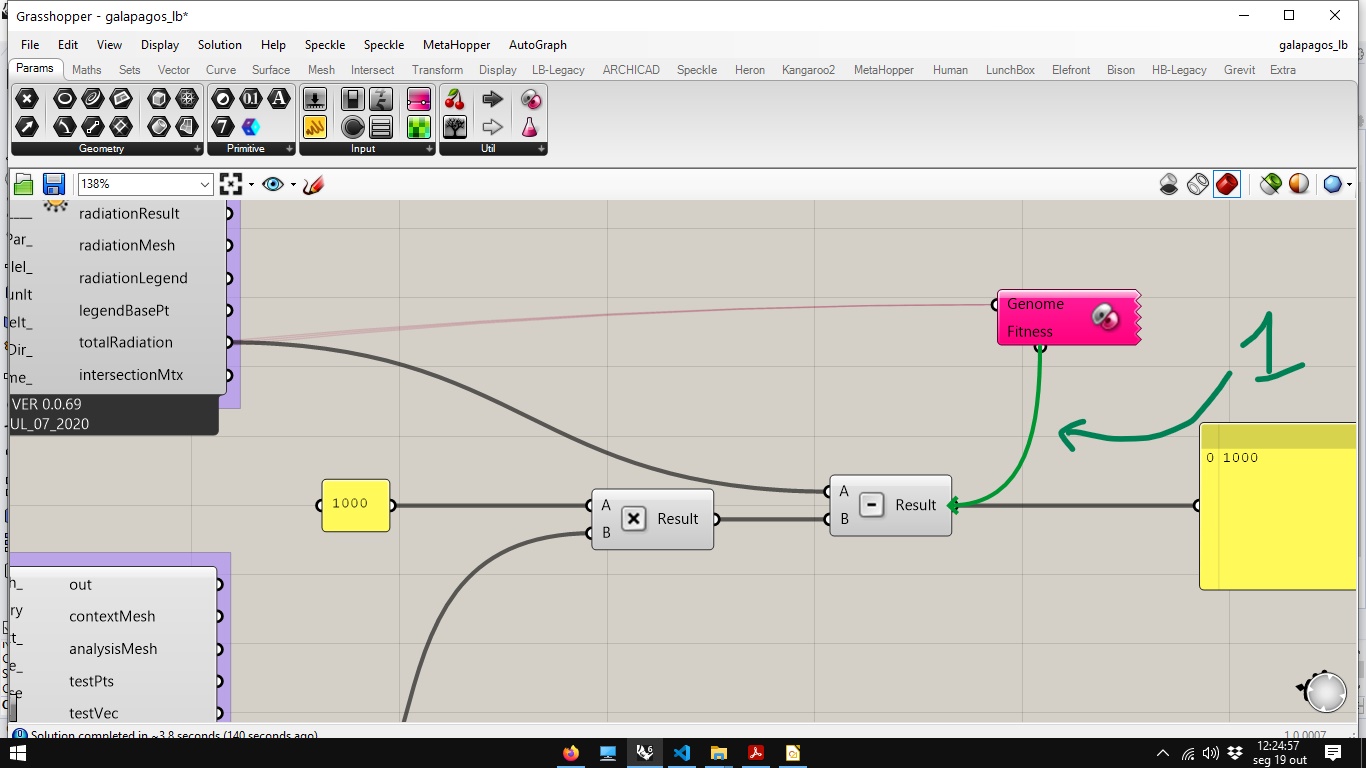
galapagos_01

To indicate the value to use as a fitness function, you must drag the connection from the Galapagos component input to the output that displays the value to be optimized.

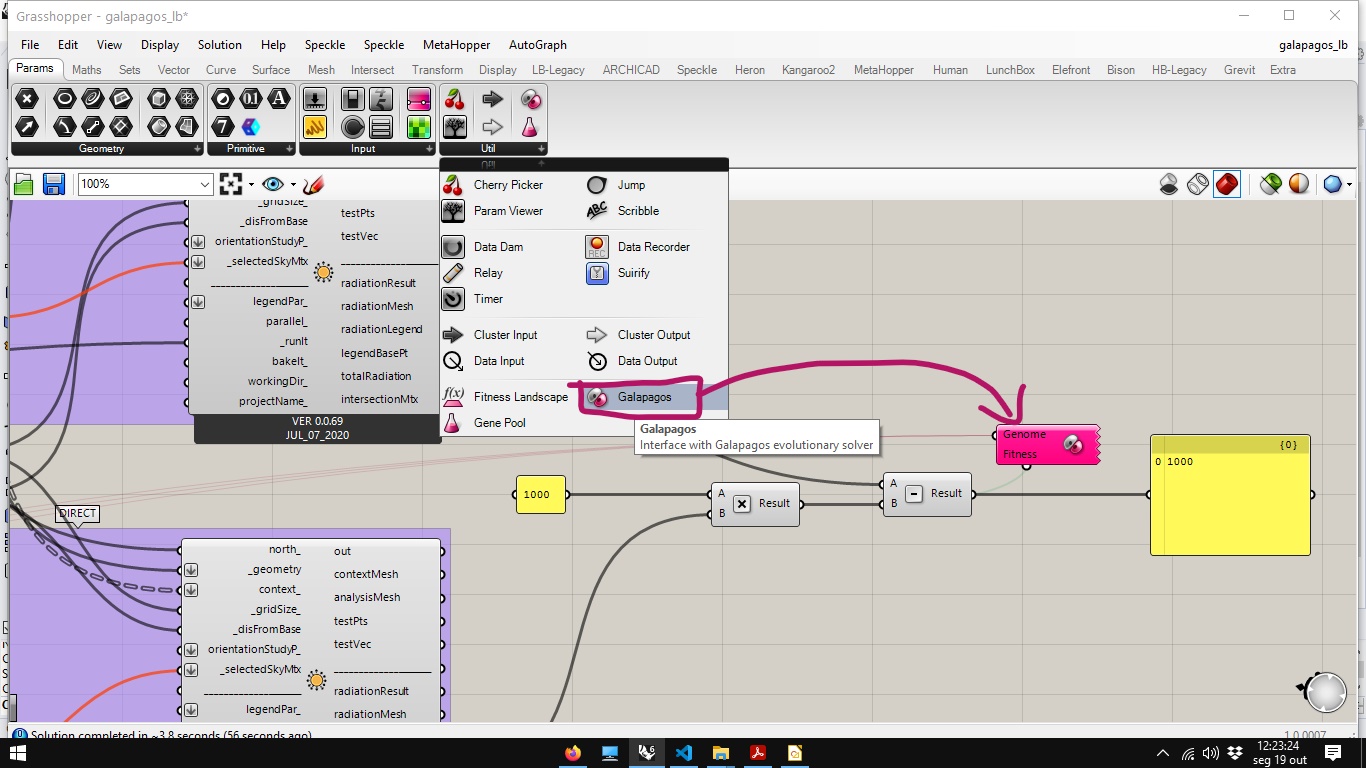
galapagos_01

Double-click the Galapagos component icon to open the solver editor.

Running the simulation

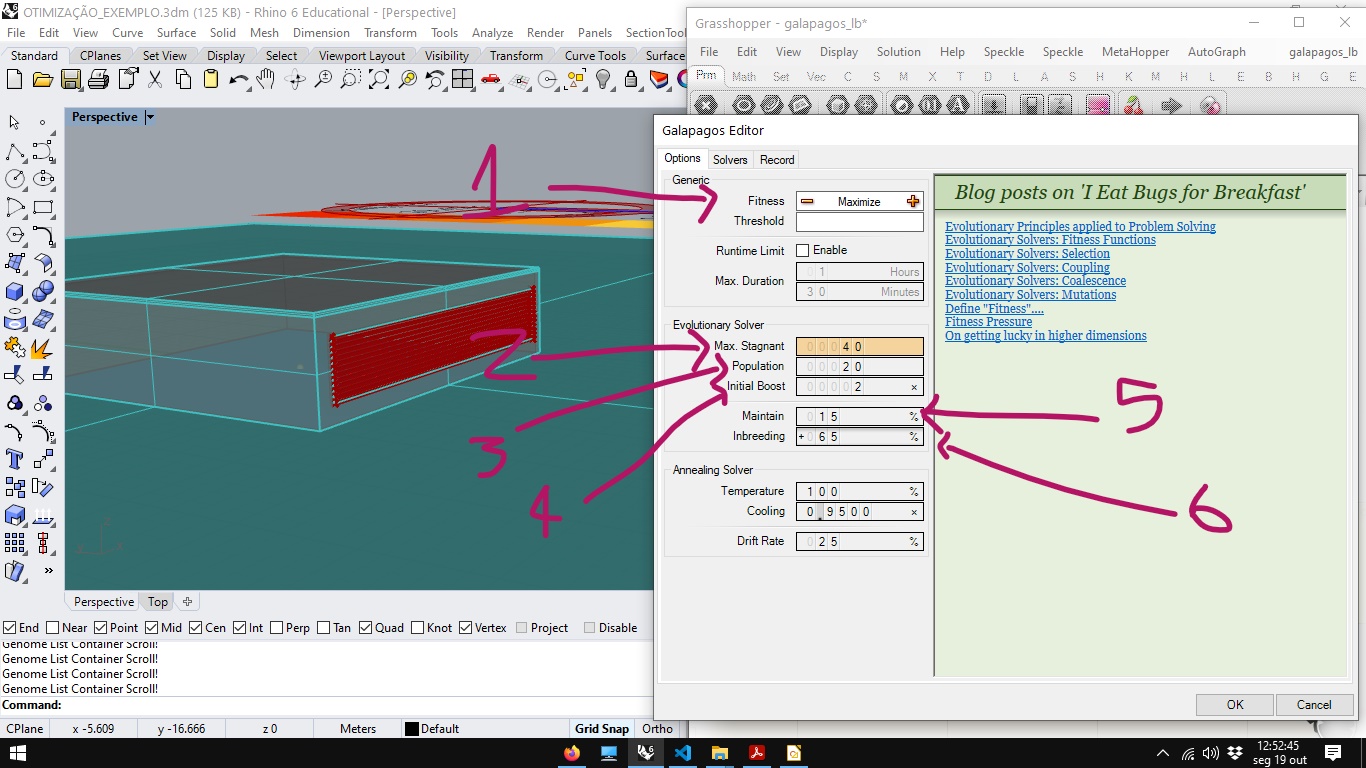
Galapagos Editor has 3 tabs: Options (to configure the analysis), Solver (to run the simulation) and Record (where a step-by-step record of a simulation is recorded). In options we can configure:

  1. If the algorithm will search for a maximum or minimum location.
  2. How many generations can be generated without evolution in the function of aptitude.
  3. The size of the population 4. How many times the initial population will be increased in the first generation
  4. The percentage of individuals to be maintained according to the criterion of the aptitude function.
  5. Percentage of individuals to be generated from the combination of genes of individuals maintained in the previous generation.

galapagos

  1. Using the genetic solver
  2. Start optimization 3. Generation diagram
  3. representation of the population
  4. representation of the genome
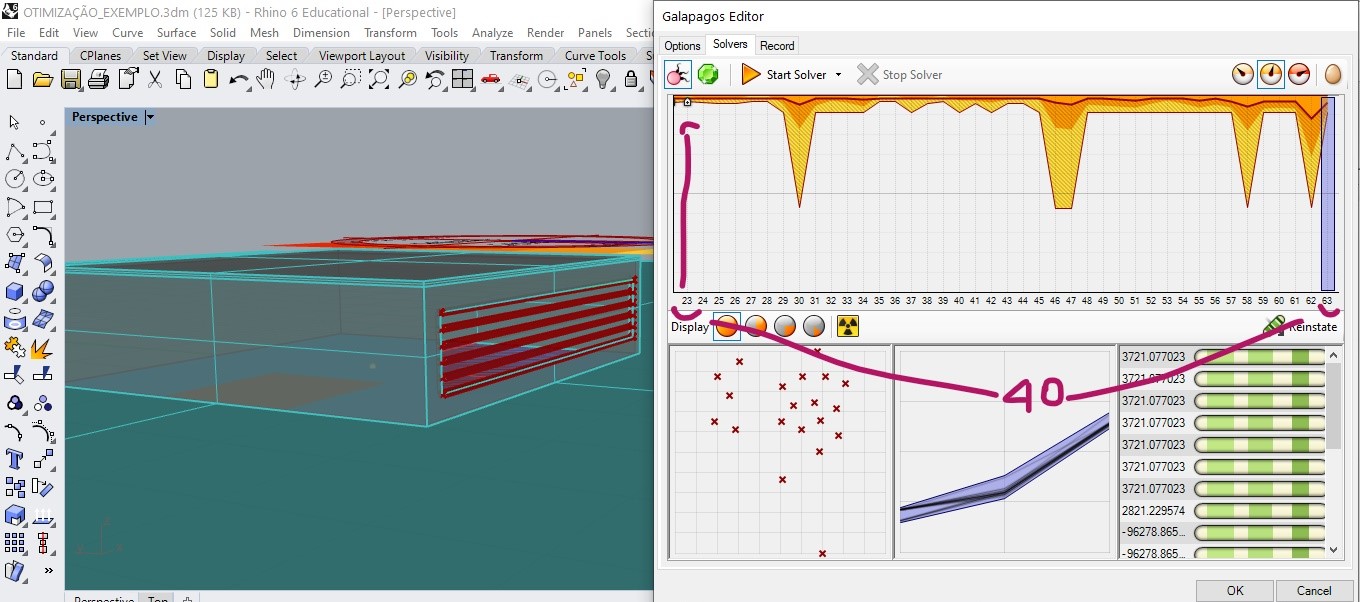
  5. representation of individuals of a generation

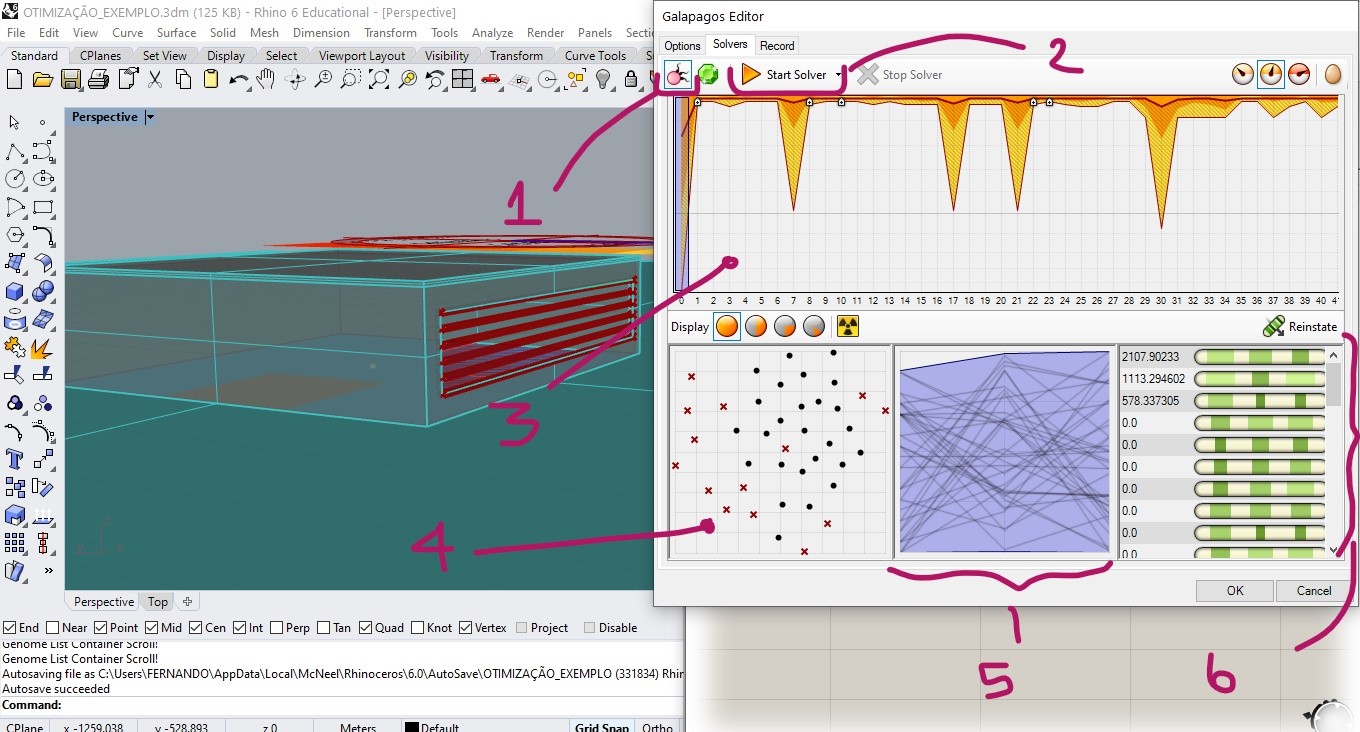
galapagos

It is possible to select a germ (1) and an individual (2) of a generation and adjust the slidres for the position of this individual (3).

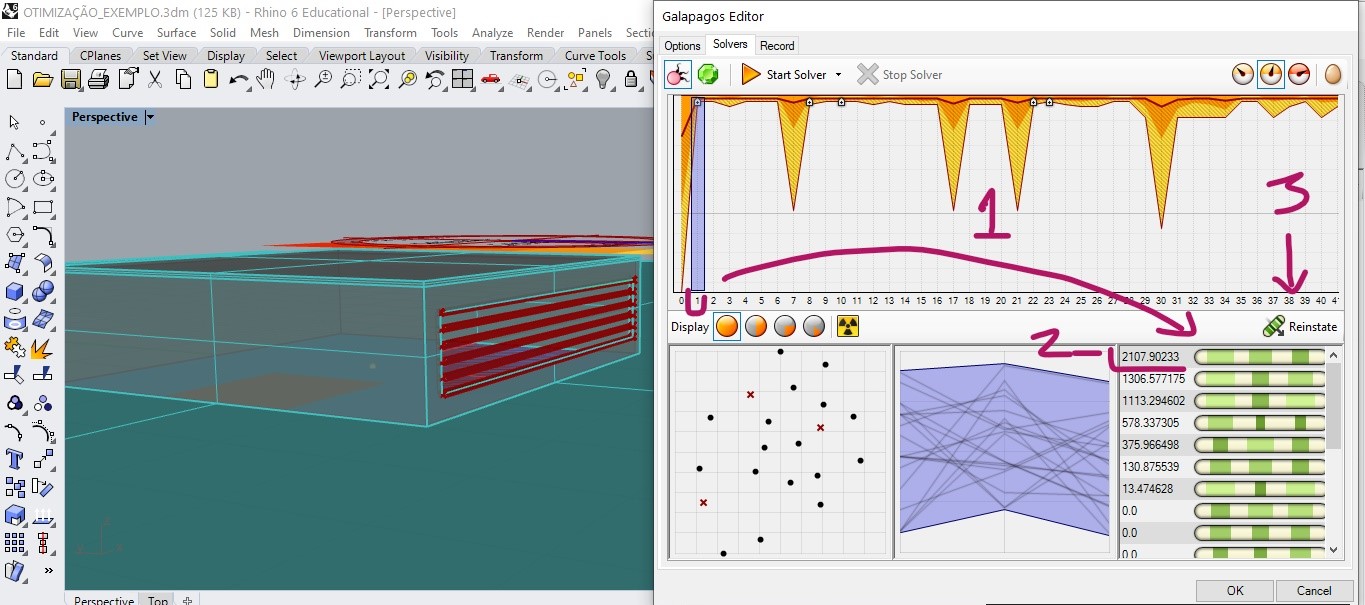
galapagos

The small + sign in the generation diagram indicates that a new value for global maximum has been found. We can see the maximum value found in generation 8 in the image below

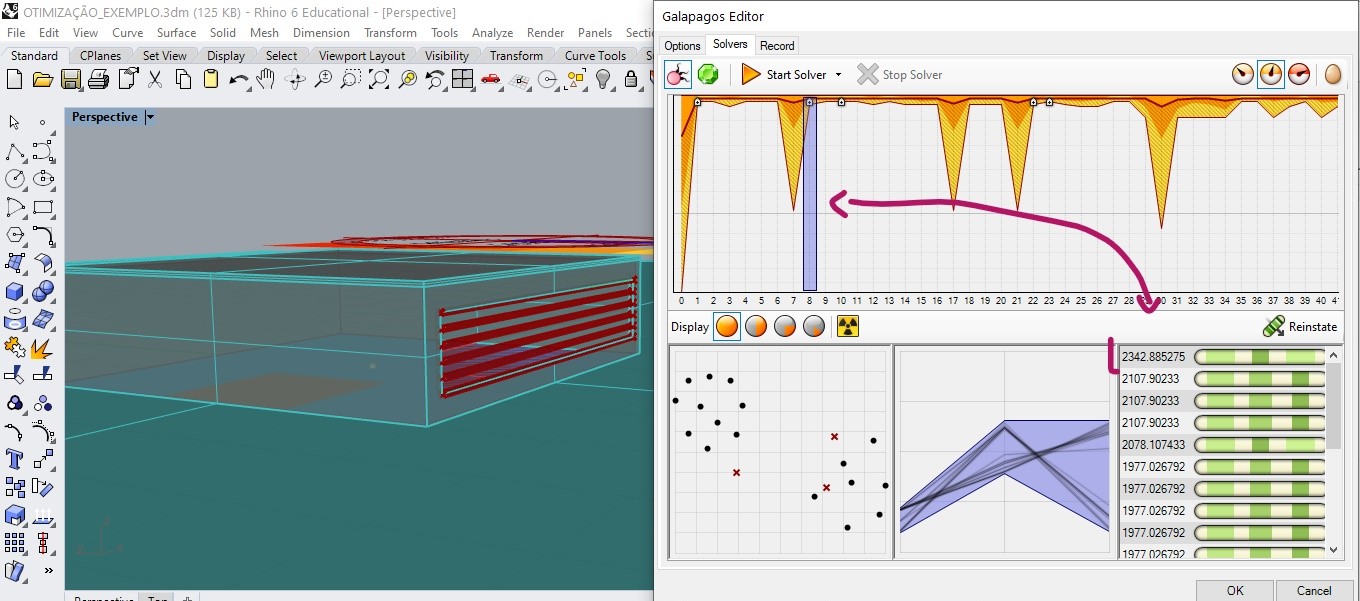
galapagos

In generation 10, another maximum value was found.

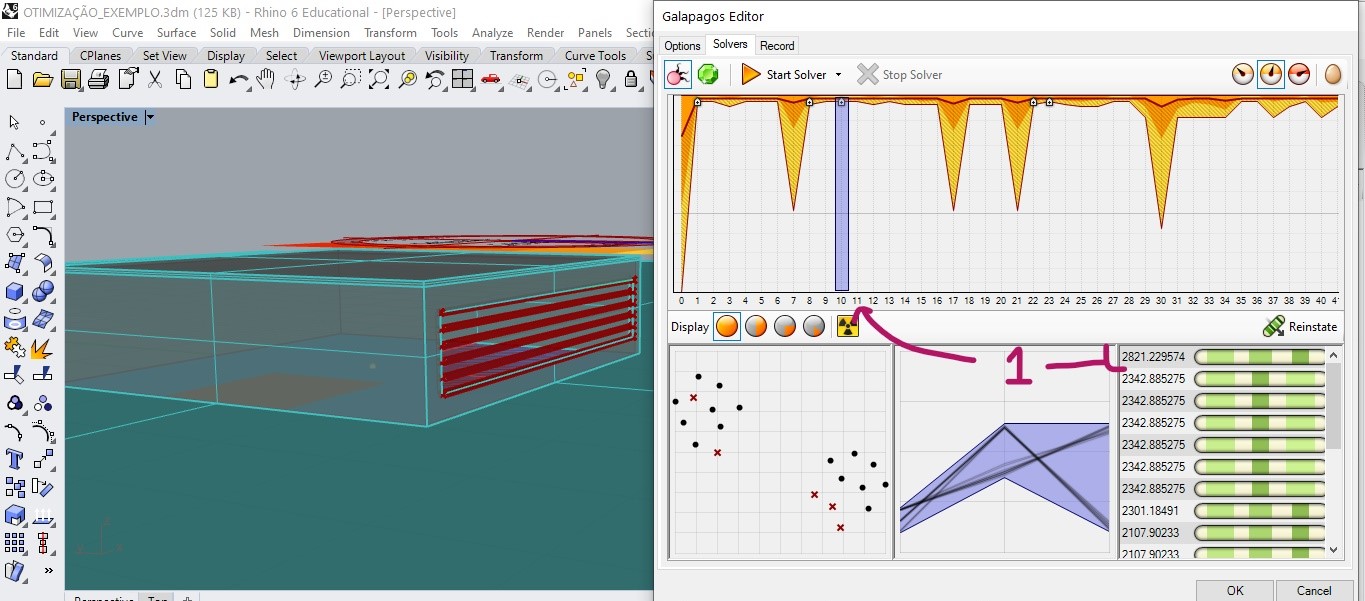
galapagos

In generation 22 a new global maximum candidate was found.

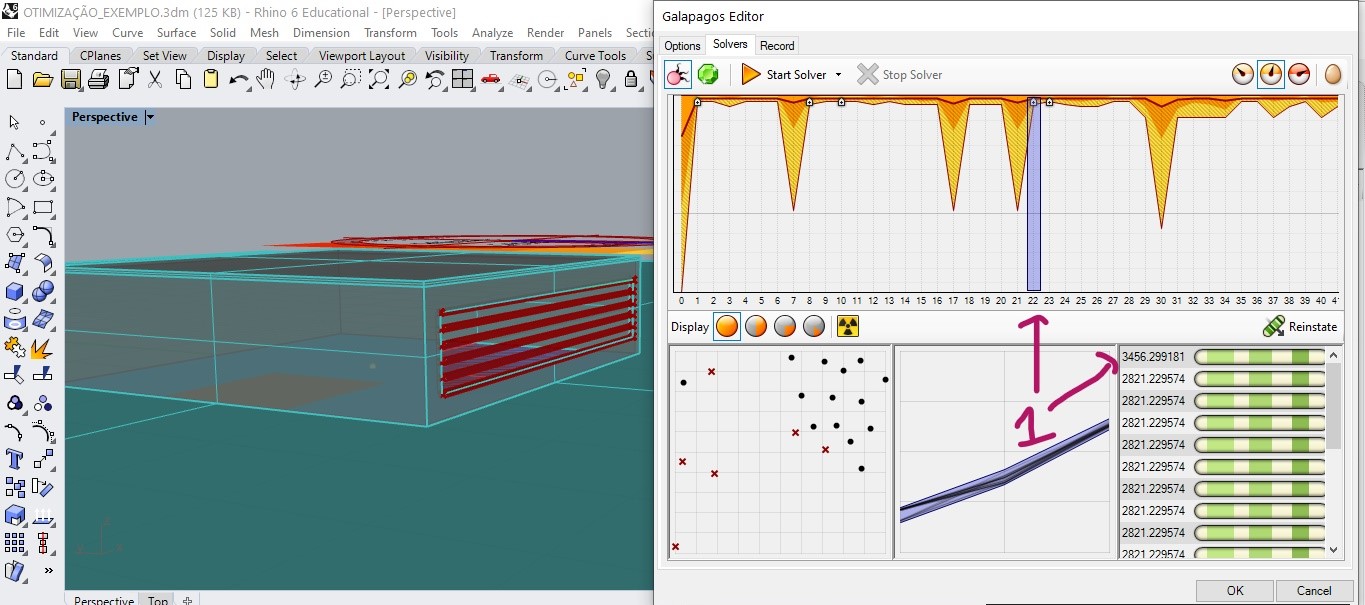
galapagos

in generation 23 a new value is found.

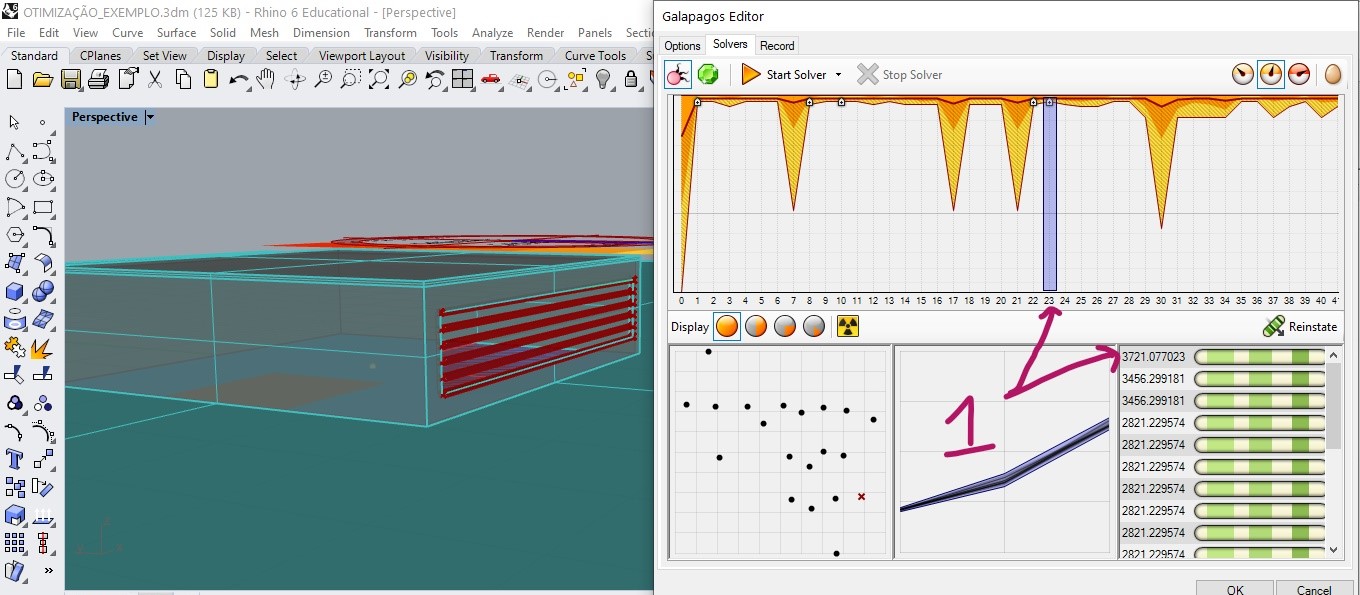
galapagos

After 40 generations without alternating the value greater than that found in generation 23, the solver reaches its stop condition.

galapagos